Компьютерная графика :: OpenGL :: Примитивы и преобразования пространства в OpenGL на примере рисования куба

Примитивы и преобразования пространства в OpenGL на примере рисования куба

Строго говоря, когда мы пишем программу, используя OpenGL, мы ничего не рисуем. Мы описываем модель сцены, задаем свойства примитивов, из которых состоят все остальные объекты, и управляем состояниями OpenGL. Визуализацией этой модели занимается OpenGL, на основе той информации, которую мы сообщили. Современные графические системы позволяют вмешиваться в процесс визуализации, используя шейдеры, что позволяет программировать достаточно гибкие и быстрые графические приложения.

Примитивы OpenGL

Посмотрим, из каких элементов (примитивов) состоит наша сцена. В OpenGL есть три типа примитивов: точка, отрезок и многоугольник. Каждый из этих объектов описывается перечислением своих вершин: координаты точки, концов отрезка или вершин многоугольника. Подробнее о примитивах будет рассказано позже, а пока остановимся на моделировании простейшей геометрии.

Четырехугольник (Quad)

На любой многоугольник в OpenGL накладываются ограничения. Первое, многоугольник должен быть простым, т.е. не иметь самопересечений. Второе, он должен быть выпуклым. В выпуклом многоугольнике отрезок, соединяющий две любые две внутренние точки, не пересекает его границы.


Невыпуклый многоугольник	Самопересечения	Корректный многоугольник

Все примитивы в OpenGL задаются с помощью следующей конструкции:

glBegin(GL_QUADS);
     glVertex3f(-0.5f, -0.5f, 0.0f );
     glVertex3f(-0.5f, 0.5f, 0.0f );
     glVertex3f( 0.5f, 0.5f, 0.0f );
     glVertex3f( 0.5f, -0.5f, 0.0f );
glEnd();

В качестве параметра команде glBegin передается тип примитивов, которые будут описываться между командами glBegin/glEnd. Внутри указываются координаты вершин примитива.

Обратите внимание на формат команды glVertex3f. Тройка означает, что команде передаются три аргумента. В данном случае это координаты в формате (x, y, z). Сигнатура f означает, что параметры этой команды имеют тип float.

Рисуем куб

void DrawCube(GLfloat size)
{
     glBegin(GL_QUADS);
     // левая грань
     glVertex3f( -size / 2, -size / 2, -size / 2);
     glVertex3f( -size / 2, size / 2, -size / 2);
     glVertex3f( -size / 2, size / 2, size / 2);
     glVertex3f( -size / 2, -size / 2, size / 2);
     // правая грань
     glVertex3f( size / 2, -size / 2, -size / 2);
     glVertex3f( size / 2, -size / 2, size / 2);
     glVertex3f( size / 2, size / 2, size / 2);
     glVertex3f( size / 2, size / 2, -size / 2);
     // нижняя грань
     glVertex3f( -size / 2, -size / 2, -size / 2);
     glVertex3f( -size / 2, -size / 2, size / 2);
     glVertex3f( size / 2, -size / 2, size / 2);
     glVertex3f( size / 2, -size / 2, -size / 2);
     // верхняя грань
     glVertex3f( -size / 2, size / 2, -size / 2);
     glVertex3f( -size / 2, size / 2, size / 2);
     glVertex3f( size / 2, size / 2, size / 2);
     glVertex3f( size / 2, size / 2, -size / 2);
     // задняя грань
     glVertex3f( -size / 2, -size / 2, -size / 2);
     glVertex3f( size / 2, -size / 2, -size / 2);
     glVertex3f( size / 2, size / 2, -size / 2);
     glVertex3f( -size / 2, size / 2, -size / 2);
     // передняя грань
     glVertex3f( -size / 2, -size / 2, size / 2);
     glVertex3f( size / 2, -size / 2, size / 2);
     glVertex3f( size / 2, size / 2, size / 2);
     glVertex3f( -size / 2, size / 2, size / 2);
     glEnd();
}

Прим. В этом примере моделируется только геометрия куба. Для правильного освещения и наложения текстуры для каждой грани потребуется задать дополнительные свойства: нормаль и текстурные координаты.

Аффинные преобразования

В статье “Аффинные преобразования в пространстве“ были подробно рассмотрены аффинные преобразования пространства. Посмотрим, каким образом они присутствуют в OpenGL.

Прим. В данной статье не рассматриваются комбинации аффинных преобразований. Об этом будет подробно написано в следующей статье.

Аффинные преобразования в OpenGL
void glTranslatef(float x, float y, float z); void glTranslated(double x, double y, double z);	Параллельный перенос на вектор (x, y, z)
void glRotatef(float angle, float x, float y, float z); void glRotated(double angle, double x, double y, double z);	Поворот против часовой стрелки вокруг вектора из начала координат в точку (x, y, z)
void glScalef(float x, float y, float z); void glScaled(double x, double y, double z);	Масштабирование в x, y, zраз по соответствующим осям

Прим. Команда glScale* может принимать произвольные аргументы, в т.ч. один из параметров может быть равен нулю. В этом случае преобразование не будет аффинным.

Если требуется применить специальное преобразование, заданное матрицей или применение стандартных команд по ряду причин не удобно, можно воспользоваться командой

glMultMatrix{fd}(const TYPE *m);

*m – указатель на массив из 16 значений типа TYPE записанных в память по столбцам. Для примера запишем код преобразования скоса:

GLfloat m[4][4] = {
     {1.0f, 0.0f, 0.0f, 0.0f},
     {1.0f, 1.0f, 1.0f, 0.0f},
     {0.0f, 0.0f, 1.0f, 0.0f},
     {0.0f, 0.0f, 0.0f, 1.0f}
};
glMultMatrixf(&m[0][0]);

Матрица этого преобразования:

| 1 1 0 0 |

| 0 1 0 0 |

| 0 1 1 0 |

| 0 0 0 1 |

Моделирование сложных сцен предполагает расположение объектов друг относительно друга, т.е. появляется иерархия объектов. В следующей статье будут рассмотрены комбинации преобразований, различные системы координат и как моделировать сцены, состоящие из нескольких объектов.

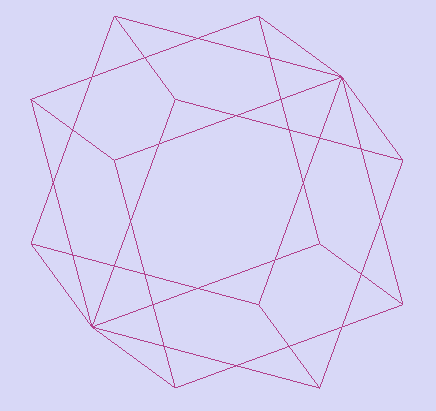
Пример. Нарисовать единичный куб, повернутый вокруг вектора (1, 1, 1) на 30 градусов.

Сразу оговоримся, что в этом примере будут использоваться некоторые команды, которые не были подробно рассмотрены. Они будут содержать необходимые комментарии.

Разберем функцию отрисовки, которая рисует единичный куб в начале локальной системы координат:

GLvoid Engine::Draw(GLvoid)
{
      glClear(GL_COLOR_BUFFER_BIT);          // Очищается буфер кадра

      glColor3f(0.7f, 0.25f, 0.55f);         // Задается текущий цвет примитивов
      glutWireCube(1.0f);                    // Рисуется проволочный куб со стороной 1
}

Прежде, чем рисовать что-то на экране, требуется его очистить. Это делается командой glClear c параметром GL_COLOR_BUFFER_BIT. Если этого не сделать, всё будет нарисовано поверх предыдущего кадра:

Далее выбираем цвет примитивов, в данном случае белый. Значение каждого из параметров должно лежать в границах 0.0 - 1.0 и представляет собой долю каждой из трех составляющих: красной, зеленой и синей. Последняя команда рисует единичный проволочный куб с центром в начале координат.

Теперь мы хотим повернуть куб на 30 градусов вокруг вектора (1, 1, 1). Казалось бы для этого требуется перед отрисовкой куба вставить команду glRotatef(30.0f, 1.0f, 1.0f, 1.0f):

GLvoid Engine::Draw(GLvoid)

{

glClear(GL_COLOR_BUFFER_BIT); // Очищается буфер кадра

glRotatef(30.0f, 1.0f, 1.0f, 1.0f); // Поворот на 30 градусов вокруг вектора (1, 1, 1)

glColor3f(0.7f, 0.25f, 0.55f); // Задается текущий цвет примитивов

glutWireCube(1.0f); // Рисуется проволочный куб со стороной 2
}

Однако такой вариант будет доворачивать систему координат при каждой перерисовке. Т.о. получим серию изображений вместо одного:


30 градусов (исходный вариант)	60 градусов	90 градусов

Решением этой проблемы будет поворот системы координат в обратном направлении после перерисовки:

GLvoid Engine::Draw(GLvoid)
{

glClear(GL_COLOR_BUFFER_BIT); // Очищается буфер кадра

glRotatef(30.0f, 1.0f, 1.0f, 1.0f); // Поворот на 30 градусов вокруг вектора (1, 1, 1)

glColor3f(0.7f, 0.25f, 0.55f); // Задается текущий цвет примитивов

glutWireCube(1.0f); // Рисуется проволочный куб со стороной 2

glRotatef(-30.0f, 1.0f, 1.0f, 1.0f); // Поворот на -30 градусов вокруг вектора (1, 1, 1)

}

У такого подхода есть несколько недостатков:

дублирование кода: исправив параметры прямого преобразования, придется исправлять их в обратном;
неточность: в процессе преобразований могут накапливаться незначительные ошибки, которые при многократных перерисовках будут заметны;

Эта проблема легко решается, если перед выполнением преобразований запомнить текущую локальную систему координат, а после отрисовки в точности восстановить её. Делается это парой команд glPushMatrix/glPopMatrix. При чём тут матрицы будет рассмотрено в следующей статье. Финальный код будет выглядеть следующим образом:

GLvoid Engine::Draw(GLvoid)

{

glClear(GL_COLOR_BUFFER_BIT); // Очищается буфер кадра

glPushMatrix(); // Запоминается локальная система координат
glRotatef(30.0f, 1.0f, 1.0f, 1.0f); // Поворот на 30 градусов вокруг вектора (1, 1, 1)

glColor3f(0.7f, 0.25f, 0.55f); // Задается текущий цвет примитивов

glutWireCube(1.0f); // Рисуется проволочный куб со стороной 2
glPopMatrix(); // Восстанавливается локальная система координат

}

Скачать исходные тексты демонстрационного приложения

Друзья

Примитивы и преобразования пространства в OpenGL на примере рисования куба

Примитивы OpenGL

Четырехугольник (Quad)

Рисуем куб

Аффинные преобразования