Мы vkontakte.ru
Друзья
Словарь синонимов русского языка
Математическое задание прямой на плоскости
В данной статье речь пойдет о задании идеальной прямой линии и отрезка. Понятие прямой линии является в геометрии исходным и определяется аксиомами геометрии лишь косвенно. В нашей геометрической модели можно отталкиваться от понятия расстояния между двумя точками. Прямой линией будем называть линию, путь вдоль которой равен расстоянию между двумя точками.Прим. В конкретной статье не будем пытаться строго определить геометрию, т.к. рассматривается практическая сторона вопроса. Но вместе с тем, хочется подчеркнуть, что строгое введение рассматриваемых понятий не является тривиальным.
Прим. Пока рассматриваются идеальные геометрические объекты, точки которых могут иметь произвольные действительные координаты.
Рассмотрим как задается прямая линия.
Уравнение прямой на плоскости в
декартовых координатах
Это уравнение позволяет задать абсолютно любую прямую на плоскости. При этом коэффициенты A и B могут обращаться в нуль, но не одновременно:
A2 + B2 > 0
Тройка чисел (A, B, C) представляет собой однородные координаты любой прямой плоскости в двумерном пространстве всех прямых плоскости. Однородные координаты в данном случае избыточны, т.к. прямую можно задать двумя числами. Принять один из коэффициентов A, B или C за единицу нельзя, так как возможен вариант равенства выбранного коэффициента нулю. Предлагается выбрать набор, в котором
A2 + B2 =
Это всегда возможно сделать, так как сумма квадратов A2 + B2 положительна, следовательно, на неё можно разделить обе части уравнения прямой с произвольными коэффициентами.
Прим. Ниже не будет использоваться факт равенства суммы квадратов A и B единице, чтобы сохранить универсальность предложенных формул.
Задание прямой по двум точкам
Ax1 + By1 + C = 0
Ax2 + By2 + C = 0
Вычитая, получаем
A(x1 – x2) + B(y1 – y2) = 0
Видно, что A = (y1 – y2) и B = -(x1 – x2) удовлетворяют этому уравнению:
(y1 – y2) (x1 – x2) – (x1 – x2)(y1 – y2) = 0
Т.о. A и В найдены. C получается из первого уравнения:
C = -(y1 – y2)x1 + (x1 – x2)y1
Существует более простая форма записи для запоминания, которая дает аналогичный результат (с точностью до знака):
x – x1 = y – y1
x2 – x1 y2 – y1
Геометрический смысл вектора (A, B) это вектор нормали к данной прямой. Данный факт легко проверить, если скалярно умножить n(A, B) на направляющий вектор l(x2 – x1, y2 – y1), который задает направление вдоль прямой.
Уравнение прямой с угловым
коэффициентом
y = -(A / B)x - (C / B)
или
y = kx + b
При построении прямых эта форма записи более удобна, чем предыдущая. Она позволяет явно показать соотвествие между x и y. Но, в отличие от математики, мы будем использовать и вариант:
x = kxy + bx
При растеризации важно, чтобы коэффициент k (kx) был меньше единицы. Тогда при изменении аргумента на 1 функция меняется не более чем на единицу. Тем самым будет обеспечиваться связность.
Пример, когда выбран k > 1:
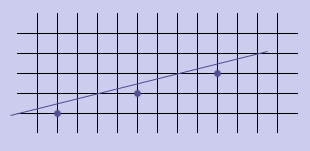
Остаются два случая
горизонтальной и вертикальной прямых. Они рассматриваются отдельно и для них
алгоритмы растеризации очевидны.
Расстояние до прямой
r(A, p) = min r(A, B), где B – точка прямой p
Возможны несколько подходов к решению задачи нахождения расстояния:
- аналитический: уравнение прямой
записывается в параметрическом виде:
y = y(t)
Затем выписывается функция расстояния r(t) от точки А до точки прямой p, определяемой параметром t, и ищется минимум. Далее считается расстояние между точкой A и точкой прямой, соответствующей минимуму функции. Оно и будет искомым по определению расстояния.
Описанный подход решает задачу ”в лоб” и является довольно трудоемким.
- геометрический:
этот
подход использует тот факт, что кратчайший отрезок между точкой А
и точками прямой p принадлежит прямой,
перпендикулярной исходной прямой p и проходящей через
точку А.
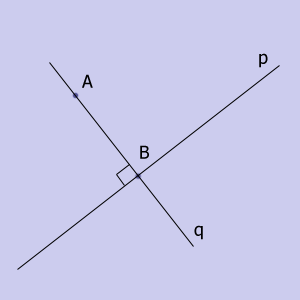
Записываем уравнение прямой q, проходящей через точку А и
перпендикулярной прямой p. Ищем точку B пересечения прямых p и q.
Искомым будет расстояние |AB|.
Этот способ менее трудоемок, чем
предыдущий и будет подробно рассмотрен в курсе теоретической геометрии.
- векторный: описание решения
поставленной задачи с помощью этого способа довольно объемное, но оно
лучше всего отражает суть вещей.
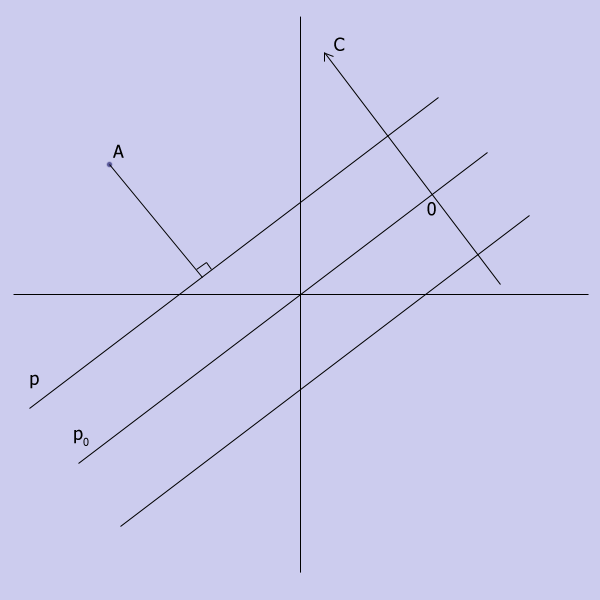
Любую прямую,
параллельную заданной, можно, при фиксированных A и B, задать свободным членом С.
Прямая, проходящая через начало координат имеет С = 0. Заметим, что расстояния от точки А до
любой из этих прямых различаются на некоторую величину, непосредственно
связанную с С. Таким образом, задачу
отыскания расстояния можно разбить на две:
- найти расстояние от заданной точки A, до прямой p0, параллельной данной и проходящей
через начало координат;
- найти расстояние от данной прямой p, до прямой p0.
Прим. В рассуждениях ниже будет использоваться тот факт, что вектор (A, B) нормален прямой, задаваемой уравнением Ax + By + C = 0.
- найти расстояние от заданной точки A, до прямой p0, параллельной данной и проходящей
через начало координат:
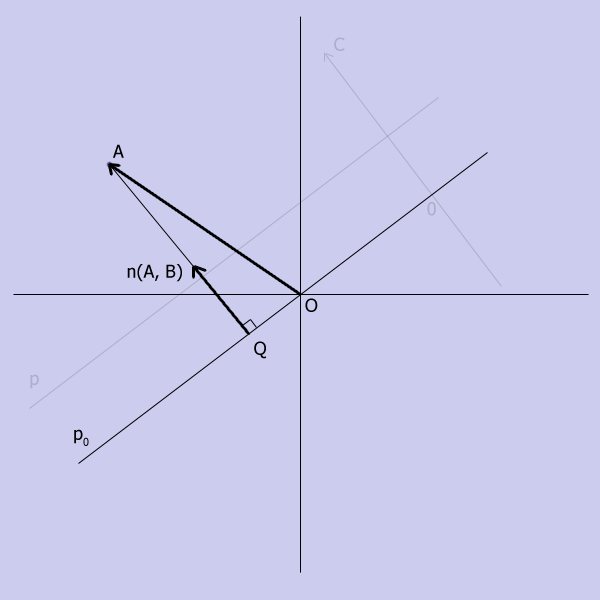
Тогда расстоянием,
в заданном смысле, будет проекция вектора OA на вектор n(A, B), равная:
(x, y) * (A, B) = Ax + By
|(A, B)| sqrt(A2 + B2)
Прим. Здесь и далее, sqrt
(сокращение от английского square root) обозначает квадратный корень.
- найти расстояние от данной прямой p, до прямой p0:
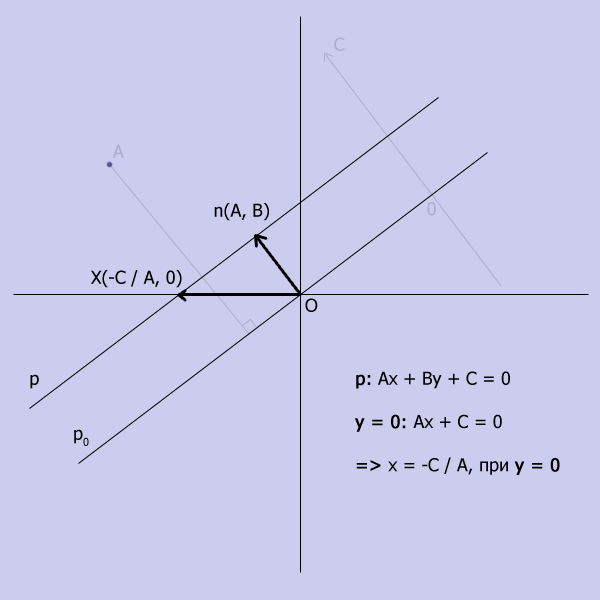
Рассмотрим
случай, когда прямая p имеет
пересечение с осью Ox (случай горизонтальной прямой
рассматривается аналогично). Тогда расстоянием, в заданном смысле, будет
проекция вектора OX на вектор n(A, B), равная:
(-C / A, 0) * (A,
B) = -C
|(A,
B)|
sqrt(A2 + B2)
Искомое расстояние
будет находиться как расстояние от прямой p0 до точки А минус расстояние от прямой p до
прямой p0. В итоге
получаем:
Ax + By + C
sqrt(A2 +
B2)
Чтобы получить
расстояние в классическом смысле осталось добавить модуль:
r(A,
p) = |Ax + By + C|
sqrt(A2 + B2)
Прим. По сути, мы использовали тот же факт, что
и при геометрическом подходе, а именно: кратчайший
отрезок между точкой А и точками прямой p будет принадлежать прямой,
перпендикулярной исходной прямой p и проходящей через точку А.
Прим. В одной из последующих статей будет рассмотрен вопрос отношения
точка/прямая и точка/отрезок, где мы подробно проанализируем смысл знака
выражения под модулем. Но, пока без объяснения, можно привести следующий факт:
Пусть дана прямая p, заданная уравнением Ax + By + C = 0 и две точки A1(x1, y1), A2(x2, y2) не лежащие на этой прямой:
- Ax1 + By1 + C и Ax2 + By2 + C одного знака, тогда и только тогда, когда точки A1 и A2 лежат по одну сторону прямой p;
- Ax1 + By1 + C и Ax2 + By2 + C разного знака, тогда и только тогда, когда точки A1 и A2 лежат по разные стороны прямой p.
Угол между прямыми
Даны две прямые p и q, заданные уравнениями:p: A1x + B1y + C1 = 0
q: A2x + B2y + C2 = 0
Чтобы найти угол между ними, достаточно вспомнить, что мы знаем нормали к этим прямым. Косинус угла между нормалями равен:
cos(np, nq) = np * nq = A1A2 + B1B2
|np||nq| sqrt(A12 + B12) * sqrt(A22 + B22)
Т.к. угол между прямыми, по определению, не может быть тупым, то косинус искомого угла между прямыми p и q будет равен модулю косинуса между нормалями.
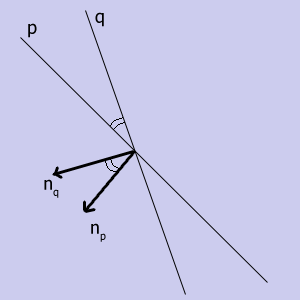
Прим. Легко видеть условие перпендикулярности двух прямых: A1A2 + B1B2 = 0.
Точка пересечения двух прямых
p: A1x + B1y + C1 = 0
q: A2x + B2y + C2 = 0
Чтобы найти точку пересечения этих прямых достаточно решить систему уравнений, задающих прямые p и q. Решая, например методом Крамера, получаем три варианта:
1) A1
= B1 = C1
A2 B2 C2
Бесконечно много решений: прямые совпадают.
2) A1
= B1 <> C1
A2 B2 C2
Решений нет: прямые параллельны.
3) A1
<> B1
A2 B2
Есть ровно одно решение: прямые пересекаются:
x = B1C2 – B2C1
; y = C1A2
– C2A1
A1B2
– A2B1 A1B2
– A2B1
Прим. В данной статье часто использовались
пропорции:
A = B
C
D
Возникает вопрос, что будет, если С или D окажутся равными нулю? В этом
случае пропорция существует в “геометрическом” смысле и выполняется, если A * D = B * C. Например, вектора (1, 0) и (2, 0) будут коллинеарны:
1 = 0
2
0
т.к. 1 * 0 = 2 * 0 – верное числовое
равенство.