Перед тем, как перейти к довольно сложной теме, а именно, заданию аффинного преобразования в матричной форме, рассмотрим следующий вопрос. Как поворачивать изображение (плоскость) с помощью мыши?

Имеется пара точек M₀(x₀, y₀), M(x, y) – начальное и конечное положения мыши. По этим точкам нужно определить угол поворота плоскости. Как это сделать. Можно попытаться экспериментировать с формулами, но вскоре станет понятно, что надо учитывать не только относительные изменения координат Δx, Δy, но и их абсолютные значения. Так, например, на приведенном ниже изображении изменения по x  для передвижений мыши M₀M и M₀’M’ совпадают, но интуитивно понятно, что одно из этих передвижений вращает треугольник по часовой стрелке, а другое - против.  

Суть приема заключается в том, что строится воображаемая единичная окружность с центром в начале координат и на ней отмеряются начальный и конечный углы. Потом производится поворот на разницу направленных углов.

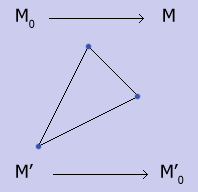
В данном случае, чтобы получить точки M₀’ и M’ надо просто нормализовать векторы OM₀ и OM. Теперь повернем плоскость, чтобы вектор OM₀’ перешел в OM'. Оказывается это не так просто, как может показаться на первый взгляд.

Угол между векторами

Посмотрим, как подсчитать угол между векторами в декартовой системе координат. Первое, что приходит в голову, это воспользоваться скалярным произведением.

Проблема заключается в том, что для скалярного произведения вектора OM^'' и OM^' будут неразличимы. Можно получить косинус угла между ними. Но если вращать плоскость от OM к OM^', то вращение идет по часовой стрелке. В случае OM^'' - против часовой. Т.о. образом кроме значения угла необходимо знать его знак. Тут может помочь “векторное произведение”.

Прим. Т.к. мы работаем в двухмерном пространстве, то строго говорить о векторном произведении нельзя. Но можно использовать тот результат, что эта операция различает порядок векторов.

Рассмотрим трехмерное пространство, причем наше двухмерное сечение это плоскость z = 0. Это означает, что все вектора в этой плоскости имеют третью координату равной 0. Векторно перемножим вектора OM(x, y) и OM^'(x’, y’):