Мы vkontakte.ru
Друзья
Словарь синонимов русского языкаЗакон Ламберта. Модель отражения Фонга. Модель отражения Блинна-Фонга
Модель отражения Фонга является довольно популярной и широкоиспользуемой в компьютерной графике, несмотря на то, что существуют более точные физические модели. Она была предложена в статье Ву Тонг Фонга (Bui Tuong Phong) в 1975 году.
Пусть заданы точечный источник света, расположенный в некоторой точке, поверхность, которая будет освещаться и наблюдатель. Будем считать, что наблюдатель точечный. Каждая точка поверхности имеет свои координаты и в ней определена нормаль к поверхности. Её освещенность складывается из трех компонент: фоновое освещение (ambient), рассеянный свет (diffuse) и бликовая составляющая (specular). Свойства источника определяют мощность излучения для каждой из этих компонент, а свойства материала поверхности определяют её способность воспринимать каждый вид освещения.
 |
+ |  |
+ |  |
= |  |
Фоновая составляющая |
Рассеянная составляющая |
Зеркальная составляющая |
Суммарное освещение |
Для удобства все векторы, описанные ниже, берутся единичными. В этом случае косинус угла между ними совпадает со скалярным произведением.
1. Фоновое освещение это постоянная в каждой точке величина надбавки к освещению. Вычисляется фоновая составляющая освещения как:
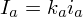 , где
, где
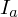 - фоновая составляющая освещенности в
точке,
- фоновая составляющая освещенности в
точке,
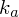 – свойство
материала воспринимать фоновое освещение,
– свойство
материала воспринимать фоновое освещение,
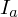 – мощность фонового
освещения.
– мощность фонового
освещения.
Из формулы выше видно, что фоновая составляющая освещенности не зависит от пространственных координат освещаемой точки и источника. Поэтому при моделировании освещения, в большинстве случае, не имеет смысла брать более одного фонового источника света. Часто просто задается некое глобальное фоновое освещение всей сцены.
2. Рассеянный свет при попадании на поверхность рассеивается равномерно во все стороны. При расчете такого освещения учитывается только ориентация поверхности (нормаль) и направление на источник света. Рассеянная составляющая рассчитывается по закону косинусов (закон Ламберта):
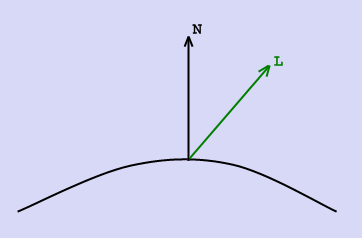
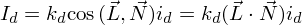 , где
, где
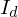 – рассеянная составляющая освещенности в точке,
– рассеянная составляющая освещенности в точке,
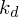 – свойство материала воспринимать рассеянное
освещение,
– свойство материала воспринимать рассеянное
освещение,
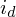 – мощность
рассеянного освещения,
– мощность
рассеянного освещения,
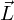 – направление из точки на источник,
– направление из точки на источник,
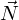 - вектор
нормали в точке.
- вектор
нормали в точке.
3. Зеркальный свет при попадании на поверхность
подчиняется следующему закону: “Падающий и отраженный лучи лежат в одной плоскости
с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол
между лучами на две равные части”. Т.о. отраженная составляющая освещенности в
точке зависит от того, насколько близки направления на наблюдателя и
отраженного луча. Это можно выразить следующей формулой:
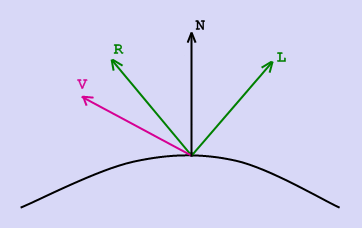
Прим. В общем случае вектора 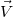 ,
, 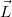 и
и 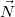 не лежат в одной плоскости.
не лежат в одной плоскости.
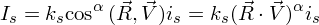 , где
, где
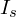 – зеркальная составляющая освещенности в точке,
– зеркальная составляющая освещенности в точке,
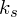 – коэффициент зеркального отражения,
– коэффициент зеркального отражения,
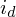 – мощность
зеркального освещения,
– мощность
зеркального освещения,
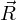 – направление
отраженного луча,
– направление
отраженного луча,
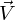 - направление на
наблюдателя,
- направление на
наблюдателя,
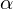 - коэффициент блеска, свойство
материала.
- коэффициент блеска, свойство
материала.
Именно зеркальное отражение представляет наибольший интерес, но в то же время его расчет требует больших вычислительных затрат. При фиксированном положении поверхности относительно источников света фоновая и рассеянные составляющие освещения могут быть просчитаны единожды для всей сцены, т.к. их значение не зависит от направления взгляда. С зеркальной составляющей этот фокус не сработает и придется пересчитывать её каждый раз, когда взгляд меняет свое направление.
Во всех вычислениях выше, для рассеянной и зеркальной компонен, если скалярное произведение в правой части меньше нуля, то соответствующая компонента освещенности полагается равной нулю.
Вычисление угла между отраженным лучом и направлением на наблюдателя
Угол между отраженным лучом и направлением на наблюдателя можно рассчитать по следующей формуле:
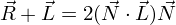
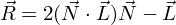
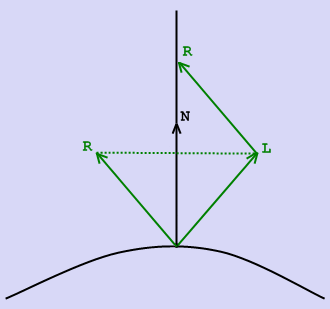
Получается это следующим образом.
Проекции векторов 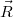 и
и 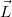 на вектор нормали совпадают и равны
на вектор нормали совпадают и равны 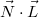 ,
следовательно, проекция вектора
,
следовательно, проекция вектора 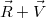 на вектор нормали равна
на вектор нормали равна 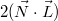 . Т.к. вектор нормали делит угол,
между падающим и отраженным лучами на две равные части, то вектор
. Т.к. вектор нормали делит угол,
между падающим и отраженным лучами на две равные части, то вектор 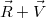 коллинеарен
вектору
коллинеарен
вектору 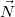 . Отсюда
получаем формулу, написанную выше.
. Отсюда
получаем формулу, написанную выше.
Скалярное произведение 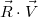 рассчитывается по формуле:
рассчитывается по формуле:
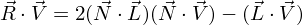
Упрощенный расчет зеркальной компоненты освещенности. Модель Блинна-Фонга
Для расчета отраженной компоненты
требуется выполнить довольно громоздкие вычисления. Существует модель Блинна-Фонга, представляющая собой модель Фонга с упрощенным расчетом зеркального отражения. Вычислим в каждой точке вектор полупути 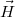 (halfway vector):
(halfway vector):
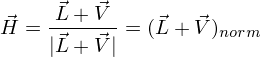
который показывает ориентацию
площадки, на которой будет максимальное отражение. Тогда величину 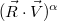 можно заменить величиной
можно заменить величиной 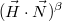 .
.
При этом α <> β и, в общем случае, соотношение между ними
зависит от пространственной связи векторов 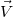 ,
, 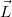 и
и 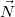 . Вектор
. Вектор 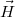 называется вектором полупути, т.к.
если все три вектора
называется вектором полупути, т.к.
если все три вектора 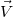 ,
, 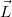 и
и 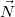 лежат в
одной плоскости, то угол между
лежат в
одной плоскости, то угол между 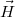 и
и 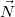 составляет половину угла между
составляет половину угла между 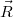 и
и 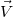 .
.
Модель отражения Блинна-Фонга никогда в точности не совпадает с моделью Фонга, однако можно подобрать соответствующие значения α и β, для которых распределения зеркальной составляющей по поверхности для обеих моделей будут очень близкими. Вместе с тем, в ряде случаев модель Блинна-Фонга требует значительно меньше вычислений, например в случае направленного бесконечно-удаленного источника.
Учет цвета
Если используется цветовая модель RGB, то все расчеты, представленные выше проделываются для каждой компоненты R, G и B по отдельности. Если при этом освещать поверхность синим рассеянным светом (0.0, 0.0, 1.0), а она воспринимает только красный рассеянный (1.0, 0.0, 0.0), то рассеянная составляющая освещенности во всех точках этой поверхности будет равна (0.0, 0.0, 0.0).
Итоги
Эта модель не учитывает способности материала излучать свет (emission), затухания света с расстоянием и не описывает модель такого источника света, как прожектор. Это описывается в следующей статье "Свойства источника света и материала. Типы источников света. Суммарное освещение".