Компьютерная графика :: Теория 3D :: Аффинные преобразования пространства

Аффинные преобразования пространства

При работе с трехмерными объектами, часто требуется совершать по отношению к ним различные преобразования: двигать, поворачивать, сжимать, растягивать, скашивать и т.д. При этом в большинстве случаев требуется, чтобы после применения этих преобразований сохранялись определенные свойства.

Определение. Преобразование плоскости называется аффинным (от англ. affinity – родство), если

оно взаимно однозначно;
образом любой прямой является прямая.

Преобразование называется взаимно однозначным, если

разные точки переходят в разные;
в каждую точку переходит какая-то точка.

Свойства аффинного преобразования в трехмерном пространстве:

отображает n-мерный объект в n-мерный: точку в точку, линию в линию, поверхность в поверхность;
сохраняет параллельность линий и плоскостей;
сохраняет пропорции параллельных объектов – длин отрезков на параллельных прямых и площадей на параллельных плоскостях.

Любое аффинное преобразование задается матрицей 3x3 с ненулевым определителем и вектором переноса:

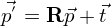
$\vec{p^{'}}=\mathbf{R}\vec{p}+\vec{t}$

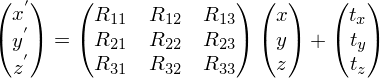
$\begin{pmatrix}x^{'} \\ y^{'} \\ z^{'}\end{pmatrix} = \begin{pmatrix}R_{11} & R_{12} & R_{13} \\R_{21} & R_{22} & R_{23} \\R_{31} & R_{32} & R_{33} \\\end{pmatrix}\begin{pmatrix}x \\ y \\ z\end{pmatrix} + \begin{pmatrix}t_x \\ t_y \\ t_z\end{pmatrix}$

Посмотрим на это с точки зрения математики. R представляет собой матрицу линейного оператора над пространством трехмерных векторов. Вектор T требуется для осуществления параллельного переноса: если помножить ( 0 0 0 ) на любую матрицу 3x3, опять получим ( 0 0 0 ) – начало системы координат, относительно преобразования R, является неподвижно точкой. Требование, чтобы определитель был ненулевой, диктуется определением. По сути, если определитель матрицы R равен нулю, то всё пространство переходит в плоскость, прямую или точку. Тем самым не соблюдается взаимная однозначность.

На практике удобно задавать аффинное преобразование одной матрицей. При этом используются однородные координаты, введенные в предыдущей статье. Аффинное преобразование будет задаваться следующей матрицей 4x4:

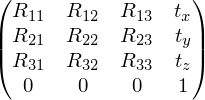
$\begin{pmatrix}R_{11} & R_{12} & R_{13} & t_{x}\\R_{21} & R_{22} & R_{23} & t_{y} \\R_{31} & R_{32} & R_{33} & t_{z} \\0 & 0 & 0 & 1 \\\end{pmatrix}$

Заметим, что первые три значения последней строки равны 0. Это необходимое условие того, что преобразование будет аффинным. В общем случае произвольная матрица размера 4x4 задает проективное преобразование. Такие преобразования, как можно догадаться из названия, используются для проецирования трехмерной сцены. Подробнее об этом будет рассказано в одной из последующих статей.

Рассмотрим частные случаи аффинных преобразований.

Прим. Здесь и в дальнейшем будет использоваться система координат, введенная следующим образом:

система координат правая;
ось z направлена на наблюдателя, перпендикулярно плоскости экрана;
ось y находится в плоскости экрана и направлена вверх;
ось x находится в плоскости экрана и направлена вправо.

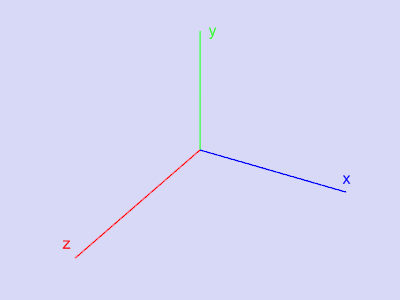
Подробнее мы остановимся на этом при рассмотрении геометрического конвейера.

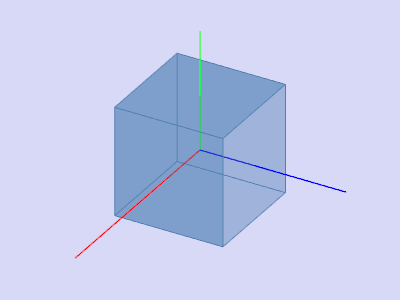
Параллельный перенос


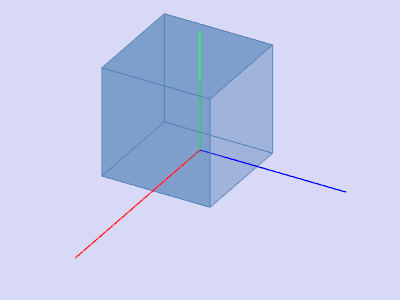
Исходный объект	Параллельный перенос

Матрица этого преобразования выглядит следующим образом:

$\begin{pmatrix}1 & 0 & 0 & t_{x}\\0 & 1 & 0 & t_{y} \\0 & 0 & 1 & t_{z} \\0 & 0 & 0 & 1 \\\end{pmatrix}$

В данном случае матрица R = E, единичной матрице.

Преобразования, рассматриваемые ниже, затрагивают только матрицу R, поэтому будет указываться только она.

Поворот (вращение)


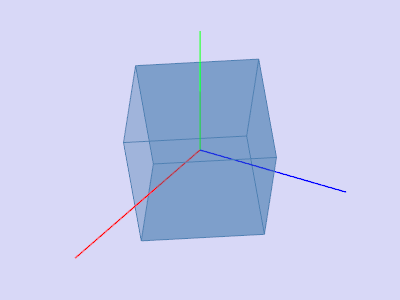
Исходный объект	Поворот вокруг некоторого вектора

Если на плоскости повороты делались вокруг некоторой точки, то в трехмерном пространстве повороты производятся вокруг некоторого вектора. Перед тем, как перейти к построению матрицы поворота вокруг произвольного вектора, рассмотрим частные случаи поворотов вокруг координатных осей.

Прим. Поворот вокруг произвольного вектора не равно поворот вокруг произвольной направленной прямой.

Поворот вокруг оси y


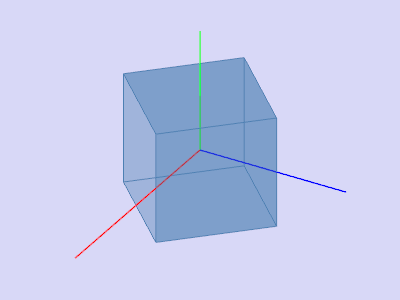
Исходный объект	Поворот вокруг оси y

Заметим, что при повороте вокруг оси yординаты точек (у-координаты) не меняются. Также стоит отметить, что координаты x и z точки преобразуются независимо от y-координаты. Это означает, что любая точка p(x, y, z) перейдет в точку p’(x’(x, z), y, z’(x, y)). Теперь осталось понять, как преобразуются координаты x и z: в плоскости Oxzэто будет поворот вокруг начала координат по часовой стрелке (т.к. x z y - левая тройка), т.е. в отрицательном направлении. Матрица такого преобразования известна (см. Поворот плоскости):

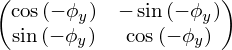
$\begin{pmatrix}\cos{(-\phi_{y})} & -\sin{(-\phi_{y})} \\\sin{(-\phi_{y})} & \cos{(-\phi_{y})} \\\end{pmatrix}$

В итоге:

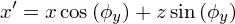
$x' = x\cos{(\phi_y)} + z\sin{(\phi_y)}$
$y' = y$
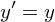
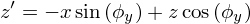
$z' = -x\sin{(\phi_y)} + z\cos{(\phi_y)}$

Матрица преобразования R_y(φ_y):

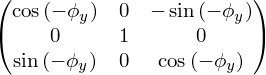
$\begin{pmatrix}\cos{(-\phi_{y})} & 0 & -\sin{(-\phi_{y})} \\0 & 1 & 0 \\\sin{(-\phi_{y})} & 0 & \cos{(-\phi_{y})} \\\end{pmatrix}$

Поворот вокруг осей x и z


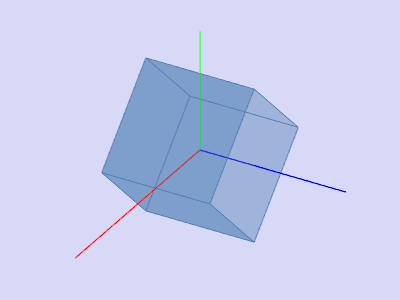
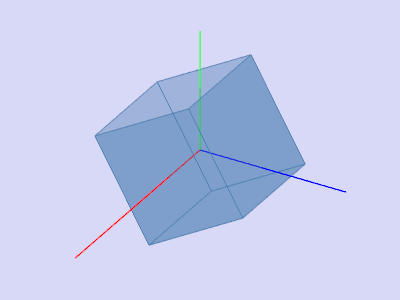
Поворот вокруг оси x	Поворот вокруг оси z

Аналогичными рассуждениями можно получить матрицы поворотов R_x(φ_x) и R_z(φ_z)вокруг осей x и z, соответственно.

Приведём окончательные результаты:

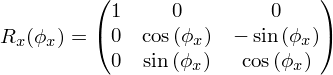
$R_x(\phi_x)=\begin{pmatrix}1 & 0 & 0 \\0 & \cos{(\phi_x)} & -\sin{(\phi_x)} \\0 & \sin{(\phi_x)} & \cos{(\phi_x)} \\\end{pmatrix}$

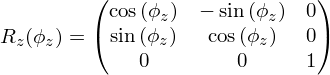
$R_z(\phi_z)=\begin{pmatrix}\cos{(\phi_z)} & -\sin{(\phi_z)} & 0 \\\sin{(\phi_z)} & \cos{(\phi_z)} & 0 \\0 & 0 & 1 \\\end{pmatrix}$

Несложно заметить, что определители матриц R_x, R_y, R_z равны 1. Также матрицы вращений R_rotобладают свойством ортогональности: R^TR = RR^T = E. Из этого, в свою очередь, следует полезное свойство, что обращение матрицы поворота можно заменить транспонированием: R^-1(φ) = R^T(φ).

Масштабирование (сжатие/растяжение, отражение)


Исходный объект	Масштабирование

Коэффициенты сжатия/растяжения, по аналогии с двухмерным пространством, определяются диагональными членами матрицы R:

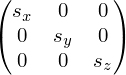
$\begin{pmatrix}s_x & 0 & 0 \\0 & s_y & 0 \\0 & 0 & s_z \\\end{pmatrix}$

Результат:

$x' = s_x x$
$y' = s_y y$
$z' = s_z z$

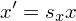
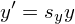
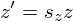
Комбинация коэффициентов s_x = -1, s_y = 1, s_z = 1 будет задавать отражение от плоскости Oyz (x = 0). При s_x = s_y = s_z = -1 получим центральную симметрию относительно начала координат.

Интерпретация матрицы R

Рассмотрим, что представляет собой матрица R с точки зрения линейной алгебры. Оказывается, что матрица R содержит базис новой системы координат.

Действительно, матрица

( R₁₁ R₁₂ R₁₃ )

( R₂₁ R₂₂ R₃₃ )

( R₃₁ R₃₂ R₃₃ )

переводит вектора декартова базиса:

( 1 0 0 ) → ( R₁₁ R₂₁ R₃₁ )

( 0 1 0 ) → ( R₁₂ R₂₂ R₃₂ )

( 0 0 1 ) → ( R₁₃ R₂₃ R₃₃ )

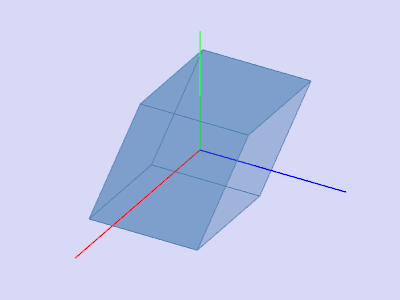
Скос


Исходный объект	Скос

Теперь несложно получить преобразование скоса. Например:

$\begin{pmatrix}1 & 1 & 0 \\0 & 1 & 0 \\0 & 1 & 1 \\\end{pmatrix}$

Прим. Если придерживаться общепринятой терминологии, то приведенное выше преобразование называется сдвигом. Сдвигом (shear) будет любое преобразование, главная диагональ матрицы R которого единичная. Если при этом определитель матрицы R равен нулю, то преобразование не является аффинным.

Сложные аффинные преобразования

Сложные аффинные преобразования можно получить как комбинацию простых (элементарных) преобразований. При этом выбирать простые аффинные преобразования можно по разному. Например, поворот можно представить как комбинацию масштабирования и сдвига. Тем не менее, для удобства, поворот также считается элементарным преобразованием. Поворот вокруг произвольного вектора представляется как комбинация поворотов вокруг координатных осей. Об этом будет подробно рассказано в следующей статье.

Друзья